新たな価値を生み出す豊かな創造性をはぐくむ算数・数学の授業を目指して
「数学的なプロセス」を重視した算数・数学の教材と授業デザイン
小・中・高等学校では現在、主体的・対話的で深い学びの実現に向けた授業改善が求められています。加藤先生は、算数・数学の授業を通して、児童・生徒における豊かな学びを具体化するために、「数学的なプロセス」を重視した教材や授業デザインの研究を行っています。
算数や数学の授業は先生から与えられた問題を解くという印象を持つ人が多いと思います。しかし、加藤先生は、児童・生徒が主体的に問題にかかわり、どのようなことが問題になりそうかを考えること、これまでの学習経験に基づいて問題をどのように解決したらよいかを考えることを大切にしています。また、単に答えを求めるだけでなく、解決した結果を振り返り、その結果から何が言えるかを考えることも大切だと考えています。その実現に向けて、加藤先生は、どのような教材が適切か、授業における教師の役割は何かに着目しています。

小学校では、台形の面積は「(上底+下底)×高さ÷2」で求められることを学習します。ここで大切なことは、先生が子どもたちに台形の面積を求める公式をわかりやすく教えることではなく、子どもたちがこれまでの学習をもとに台形の面積を求める方法を考えることです。
例えば、すでに学習した平行四辺形の面積の求め方をもとに、台形の面積を求めることができます。図のように、求めたい台形と合同な台形をつけると平行四辺形ができます。平行四辺形の面積の求め方はすでに学習しているので、面積を求めることができます。ただ、このままでは台形2つ分の面積を求めていることになるので、求めた面積を2で割る必要があります。この一連の問題解決の過程を振り返ると、「底辺×高さ÷2」という式が導き出されます。このとき、「底辺」は「上底」と「下底」をたしたものなので、「底辺×高さ÷2」の式の「底辺」を「上底」と「下底」で置き換えると、「(上底+下底)×高さ÷2」の式を導くことができます。
このように、加藤先生は、子どもたちにとって未知のことを、既知のことをもとにして解決できるような授業を大切にしています。
「文脈」と「状況」の設定の大切さ

算数・数学の授業において、数学的なプロセスを重視するためには、「文脈」と「状況」の設定が大切だと加藤先生は言います。小学校で学習するひき算では、単に計算の方法を学習するだけではなく、日常生活から問題をみいだすこと、みいだした問題を解決すること、解決した結果を日常生活に関連づけて意味づけることが大切です。
例えば、子どもたちにいす取りゲームの写真を見せると、彼らの経験に基づき「いす取りゲームをしている」「子どもが○人いる」「○人の人が座れない」などと話し始めることが考えられます。そこで、「座れない人がいるとはどういうことか」と問うと、子どもたちは子どもの人数といすの数の違いに目を向けます。そして、「違いはいくつか」と問題を焦点化するとひき算の問題をみいだすことができます。具体物や絵、図などを用いながら問題を解決し、「4」という結果を得ます。そして、その「4」が何を示しているかについて、いすとりゲームの場面に戻って考えます。すると、その「4」は座れない子どもの人数であることがわかります。
つまり、教師から問題を与えるだけではなく、子どもたちが自ら問題をみいだすことができるような、子どもたちが解決してみたいと思えるような文脈や状況を設定することが大切だということです。
「秋田県の小・中・高等学校、特別支援学校の先生方をはじめさまざまな先生方と連携・協働しながら、数学的なプロセスを重視した算数・数学の教材と授業デザインに関する研究をすすめ、秋田県をはじめ東北地方に、そして全国に発信しています」
算数・数学の授業における効果的なICTを活用
算数・数学の授業におけるICT活用も加藤先生の研究テーマの一つです。現在、小・中・高等学校では、児童生徒にタブレット端末が一人一台配布されています。加藤先生は、児童・生徒の数学的に考える資質・能力を育成することに、ICTがどう関わるかという視点で研究をしています。
ここで、中学2年生の図形の問題について考えてみましょう。以下は、図形の証明の問題です。
Q:平行四辺形ABCDの対角線の交点をOとします。辺AD上に点Pをとり、2点O、Pを通る直線をひきます。直線OPと辺BCの交点をQとします。
このとき、OP=OQとなることを証明しなさい。
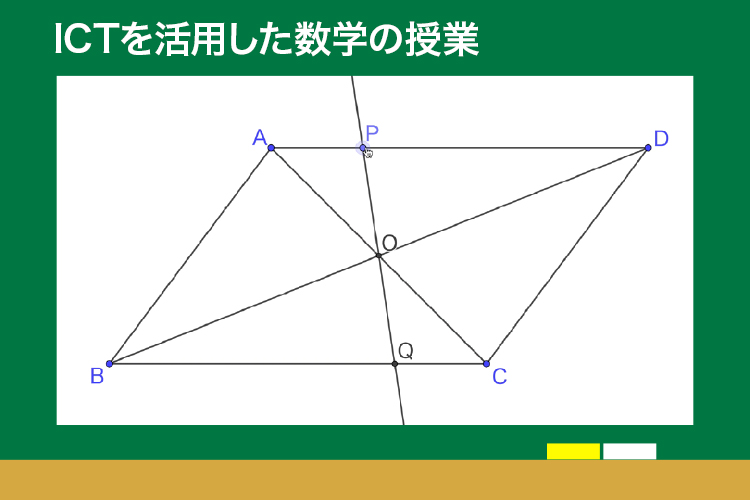
ICTを活用すると点Pを実際に動かすことが出来る
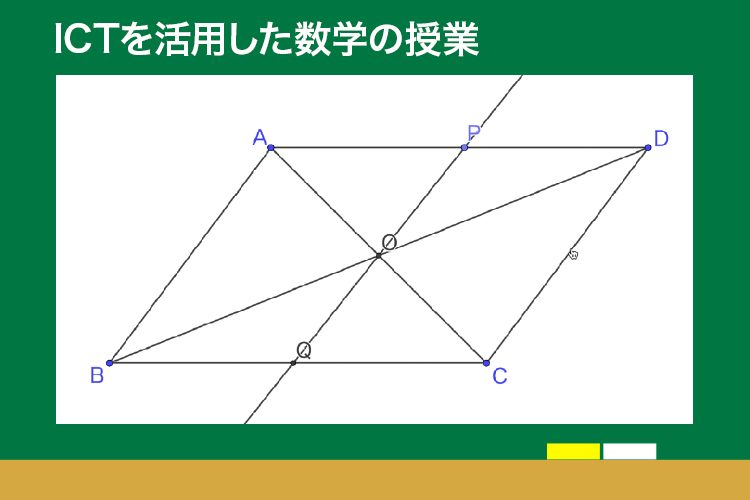
この問題は、OP=OQとなることを証明する問題ではありますが、加藤先生は、ICTを活用することによって、生徒が自ら問題をみいだしそれを解決する授業になると考えています。
「上の問題文をもとに図をかくとき、点Pをとる位置によって、図が変わります。そのため、最初からOP=OQとなる証明を考えるのではなく、点Pをとる位置によって、図がどのように変わるかについて、生徒が捉えることが大切です。タブレット端末では、画面上で、点Pを、辺AD上を動かすことができるので、生徒が点Pを動かしながら、変わっていること、あるいは変わっていないことを観察します。いくつか変わらないことはあるのですが、そのなかで、ある2つの線分の長さが変わらないのではないかと気づく生徒がいるかもしれません。そこで生徒は、点Pの位置が変わっても、OP=OQになるのではないかと、成り立つ事柄を予想します。そして、予想した事柄がいつでも成り立つかどうかを確かめるために証明することが必要になります」
と加藤先生は話し、与えられた命題が成り立つかどうかを証明するだけではなく、生徒が成り立つ事柄を予想する活動も大切であると考えています。その活動を促進するために、ICTを活用することが効果的であると考えています。図を静的に捉えるだけではなく、動的に捉えることによって、例えば、上の問題の平行四辺形ABCDを長方形ABCDに変えても、いつでもOP=OQになるといえるかどうかについても考えることができ、生徒が自ら問題を発展させて考える契機になるそうです。
数学的な見方・考え方を働かせて日常生活や社会の事象を考察することの大切さ

教科書の問題や全国学力・学習状況調査の問題の分析を行ったり、普段の生活のなかで数学的な見方・考え方を働かせて事象を考察したりすることによって、教材を開発することがあるそうです。
前者では、様々な問題を目にして、その本質は何か、意図は何かを知ることが重要だと加藤先生は言います。
そして後者には、折戸式のバスに乗っていたときに、混雑で扉が開かなかったという加藤先生自身の経験があります。その理由を知るためにバス会社に問い合わせたところ、バスは入口にセンサーがついており、安全のため特定の場所に立つとドアが開かない仕様になっていたそうです。
「バスのドアが開閉するときにえがく軌跡を考えれば、安全な立ち位置を探ることができると思いました。当時勤めていた学校では生徒がバスを利用する機会があり、生徒たちにとっても身近な話題であるので、数学Ⅱの図形と方程式の単元で教材化し、授業を構想・展開することにしました。『バスに乗っていたらドアが開かなかった。なぜだと思う?』と問いかけると、日常的にバスを利用する生徒は『見たことある』や『前にいると開かない』という経験と関連づけ、『どこに立つと開かないのだろうか』と、生徒自ら問題をみいだしていました。そして、生徒はバスのドアを平面図形として捉え、ドアの動き方を単純化・理想化して考えていました」
算数・数学を学ぶたのしさを

以前、加藤先生が「生活の中の算数・数学」というテーマで市民に向けた公開講座を行った際、中学生から70代までの方が参加してくれたそうです。公開講座では、体験活動を通して、身近にある算数や数学について学ぶことできる内容だったそうです。
「70代の方にもこのような授業は受けたことがないと非常に興味を持っていただき、今までとは違う視点で考えることも大事であるという感想をいただけたことは大変うれしかったです」
私たちの身の周りには、算数や数学に溢れています。そのことに気付くことができれば、私たちも普段とは別の視点で物事をみることができるかもしれません。加藤先生は、今後も算数・数学をより身近に感じ、算数・数学を学ぶたのしさを実感しながら一人ひとりが自分で考える力を養えるよう様々な事象を探りながら研究に活かしていくことでしょう。
研究室の学生の声
教育文化学部 学校教育課程 理数教育コース 4年次
伊藤 光希 さん

私は一番好きな教科が数学だったこと、友人に数学を教えるのが楽しかったこと、そして恩師の姿に憧れ教員を志しました。現在はICTを活用した高校数学の授業改善に関する研究をしています。
最近はGIGAスクール構想の実現に向けて、生徒が1台ずつタブレットを持ち、校内にWi-Fiを整備するなど学校のICT環境の構築が進んでいます。しかしその一方、現場の先生からは「授業でICTをどう使えば効果的か分からない」という声があるのも現状です。
私は、タブレットで問題などをただ提示するだけでなく、生徒の数学的に考える資質・能力を育成するために、ICTを効果的に活用できる教員を目指しています。現在は、高校数学で三角比を学習するときに、三角比の概念を理解することに、ICTがどのようにかかわるかについて研究をすすめています。ICTを活用した三角比の授業を構想し、秋田県内の高校で実践し、検証することを予定しています。
教育文化学部 学校教育課程 理数教育コース 4年次
村田 希良々 さん

将来は子どもと関わる仕事がしたいと思っていましたが、それを決定付けたのは中学の数学の授業での体験でした。三角錐の体積の公式を考える授業で、先生がその場でバケツに水をいっぱい入れ、角柱と底面積と高さが同じ角錐の入れ物で角柱に水を入れていくと三回で水がいっぱいになり、三角錐の体積の公式には1/3が入ることを体感させてくれたのです。このように、児童たちが「なるほど」と思える授業を自分もしたいと思い、小学校の教師を目指しています。
現在は、小学校算数科の授業で、関係的理解を促進する指導法を研究しています。関係的理解とは、例えば、速さは道のり÷時間で求められますが、単にその式を用いて速さが求められるだけではなく、それは1秒間、あるいは1分間、1時間にどのくらい進んだかということで速さを捉えていると理解していることをさします。
全国学力・学習状況調査に、「りんごジュースの量を半分にした時に果汁の割合はどのように変化するか」という問題があります。この問題では、多くの児童がりんごジュースの量を半分にすると果汁の割合も半分になると答えています。しかし実際は、量が変わっても果汁の割合は変わりません。このような課題は、比や割合を関係的に理解することに困難が生じていると考え、その改善に向けて研究をすすめています。
教育文化学部 学校教育課程 理数教育コース 4年次
菊池 亜美 さん

私は、生徒の問いを軸にした授業の実現を目指して、教師の発問に着目した授業デザインを研究しています。教師から一方的に問題を押し付けられると生徒も機械的に問題を解くことになります。生徒同士、あるいは生徒と教師の対話を通して、生徒の考えてみたい、を大切にして、それを活かすことができる数学の授業を目指しています。
全国学力・学習状況調査の結果から、事象を数学的に解釈して問題を解決することが課題となっています。例えば、1日ごとのダムの貯水量を1次関数とみなして捉え、問題を解決することに課題があることが示されています。このように、事象を数学的に解釈して問題を解決することにおける課題を克服するためには、与えられた問題を解決するのではなく、対話を通して生徒が問いをもち、その問いを軸にして授業を展開することが大切です。その授業の実現に向けて、生徒の思考を促進する教師における発問の役割について研究しています。
私が教師を目指したのは、人のためになる仕事に就きたいと考えていたとき、高校の恩師に勧められたのがきっかけです。私は数学が一番好きで得意だったので数学の教師を目指していましたが、数学にマイナスなイメージを持った人が周囲には多く、それを払拭したいという思いで秋田大学に入学しました。理数教育コースは数学が好きな人が多いので、皆で語り合ったり一緒に問題を解いたりすることが一番楽しいです。
(取材:広報課)
※掲載内容は取材時点のものです



